Актуальность. Сердечно-сосудистые заболевания, несмотря на значительные успехи, в их лечении и профилактике, остаются основной причиной высокой смертности и инвалидизации населения во всём мире [5, 9, 10]. Одно из ведущих мест в структуре смертности от болезней системы кровообращения занимает гипертоническая болезнь, особенно если она протекает на фоне сахарного диабета [2-9]. Частые осложнения и высокий уровень летальности обусловливают научную и практическую значимость поиска эффективных методов лечения при этом заболевании. Поэтому данное обстоятельство делает крайне затруднительным прогнозирование исхода гипертонической болезни, её осложнений и оптимизацию лечения пациента без привлечения математических методов, что и обусловливает необходимость формирования алгоритмических подходов к прогнозированию развития данного заболевания и его осложнений, оптимизации лечения на основе многомерного статистического моделирования [3,4].
Математическая модель может являться результатом формализации процесса, то есть построения четкого описания процесса с определённой степенью приближения к действительности [3,4].
При изучении любого процесса методом моделирования основной задачей является в первую очередь построение математического описания (математической модели) изучаемого процесса.
Материалы и методы. Случайный характер протекания процесса чаще всего объясняется действием на его элементы случайных изменений, возникающих внутри системы или вне ее, или случайным характером исходной информации, перерабатываемой системой в процессе функционирования [3, 4, 5, 6, 7]. Процессом функционирования системы проходит при последовательной смене необходимых состояний изучаемой системы во времени. Любое количественное изучение процесса (а тем более построение математической модели) возможно в случае, если определяются те величины, которые в полной мере характеризуют процесс с количественной точки зрения. Поэтому каждое состояние системы, соответствующее фиксированному моменту времени, описывается следующей формулой Y=(Y1, Y2, …, Yn), выражающей основные свойства системы с требуемым приближением к действительности. При переходе от одного мгновенного состояния системы к другому значения величин Y в общем случае меняются. Характеристики процесса можно также определять как координаты точки в n-мерном пространстве, где каждому мгновенному состоянию процесса соответствует определенная точка.
Цель математического исследования состоит в качественном описании и выявлении явных отличительных признаков, изучаемых совокупностей, на основе данных наблюдений множества Y.
Полученные результаты и их обсуждение. Не всегда признак, оказавшийся наиболее важным при одномерном рассмотрении, обнаруживает те же свойства при использовании многомерного критерия. Причем может возникнуть даже такая ситуация: на отдельно взятые признаки, когда выделенные факторы не оказывают значимого влияния, и поэтому при традиционном одномерном подходе эти признаки могут быть исключены из содержательного анализа. Однако при их рассмотрении в совокупности порой получаются чрезвычайно выразительные результаты.
Общая математическая задача формируется следующим образом: имеются объекты, характеризуемые набором случайных величин Y1, Y2, ..., Yp (многомерный вектор) с матрицей ковариаций (априори известной, либо оцененной по выборочным данным) и математическими ожиданиями, равными нулю. Это означает, что переменные Yi - стандартизованы. В нашем случае объектами являются пациенты с установленной гипертонической болезнью, протекащей на фоне сахарного диабета, которым проводилась терапия метаболическими и кардитропными препаратами и классифицированные по двум факторам – лечебной процедуре (группа) и день с начала назначения лечения (день).
При использовании объекта или признака, их условно называют матрицей «объект-свойство» или «объект-признак» и применяют прямоугольную таблицу, которая состоит из значений признаков свойств выборки наблюдений. В данной таблице одно наблюдение записывается в виде отдельной строки, которая состоит из значений используемых признаков, а каждыйотдельный признак в такой матрице представлен столбцом, состоящим из значений этого признака.
Каждому из n объектов соответствует p переменных, обозначения которых представлены в табл. 1.
Таблица 1. Значения признаков свойств выборки наблюдений
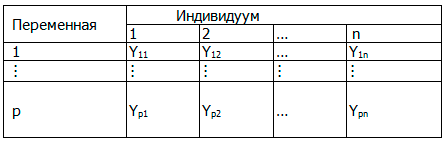
Математическое моделирование процесса лечения проводили с использованием методов главных компонент и многомерной классификации.
Построение математической модели представляет собой необходимый шаг любого серъезного исследования процесса. Однако на этом исследование не заканчивается. Дальнейшим важным шагом является использование математической модели для получения общих закономерностей, связанных с исследуемым процессом, или конкретных числовых зависимостей между параметрами.
Пусть вектор Yinx1 = (Yli,…,Yin)’ соответствует n независимым измерениям i-й переменной, i =1, …., p. Для каждого такого вектора соответствует одномерная линейная модель.
![]()
Здесь (X’)nxm– матрица ранга r≤m<n, σii – дисперсия i-й переменной и βimx1 =(βil,…, βim) ) – вектор из m-неизвестных параметров, которые соответствуют каждой переменной. Далее, p-линейные модели, которые задаются формулами (1), вместе, составляют обобщенную многомерную линейную модель. При этом матрица одинакова для всех переменных, а векторы βi могут быть различны. Зависимость переменных определяются формулой
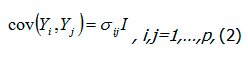
где σij – ковариация между i-й и j- й переменными. И наконец, предполагается, что p≤n-r и m<n.
Модель, задаваемую соотношениями (1) и (2), представляется в виде
![]()
где

И наконец, enxp - матрица, строки которой составляют случайную выборку размера n из невырожденного p-мерного N (0, Σ) распределения , где – Σpxp –ковариационная матрица, а 0px1 –нулевой вектор. Уравнение (3) является записью многомерной обобщенной линейной модели.
Оценкой βi служит МНК-оценка, которая использует наблюдения только переменной Yi [2].
В результате, аналогично одномерной линейной модели, оценка параметра получается в результате решения системы нормальных уравнений
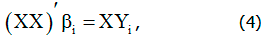
Где i= 1, …, p.
Матрица данных является основой прикладного многомерного анализа. Она представляет собой количественное выражение интересующего исследователя явления. Чтобы адекватно отражать изучаемую проблематику эта матрица должна содержать достаточное количество информации. При формализации задачи следует определить набор признаков, отражающих изучаемое явление. Все переменные измерить невозможно, поэтому приходится прибегать к тем или иным способам предварительного отбора [3, 4].
Выводы. Начало изучения какого-либо объекта характеризуется недостатком определённого набора информации о существующих в объекте зависимостях между исследуемыми переменными. Это означает, что кроме проверки наличия существенности предполагаемых зависимостей, с помощью статистическихметодов может быть установлено наличие ранее неизвестных зависимостей. Умение использовать новые зависимости позволяет генерировать новые гипотезы о механизмах исследуемых факторов воздействия на изучаемые системы.
