Введение. Для проектирования фиксирующих устройств, а также для разработки лечебных методик послеоперационной и посттравматической реабилитации травматологических больных необходимо знать величины и направления сил реакции, создаваемых весом тела, возникающих в суставах при перемещении пациента, в частности, при ходьбе. Для расчета изменения сил во времени необходимы кинематические соотношения, описывающие движения сегментов тела человека при заданной локомоции.
Несмотря на большое число исследований, посвященных ходьбе и ритмическим движениям человека, эти акты не описаны в аналитической форме, что приводит к необходимости проведения вычислительных экспериментов, направленных на создание аналитических зависимостей.
Существуют задачи, сопряженные с данной проблемой, например: задача хранения данных, имеющих отношение к математической модели процесса, а также задача представления результатов исследования в удобном для анализа формате. Комплекс поставленных задач требует разработать специализированную информационно-аналитическую систему, дающую возможность формализовать, описать и прогнозировать реакции в суставах опорно-двигательного аппарата (ОДА) человека при ходьбе.
Постановка задачи. При анализе кинематики и динамики ходьбы значительно сократить объем необходимых натурных измерений позволяет компьютерное моделирование. Если компьютерная модель адекватно отражает состояние и динамику реальных объектов, то многие необходимые сведения можно получать с помощью такой модели, избегая натурных измерений, с существенно меньшими затратами времени, а возможно, и при более низкой стоимости. Для поддержки таких моделей служит класс систем обработки данных ─ информационно-аналитические системы (ИАС).
Цель работы – создание ИАС, предназначенной для исследования кинематических и динамических характеристик двуногой ходьбы и содержащей следующие функциональные подсистемы: подсистему математического моделирования, подсистему трехмерной визуализации, подсистему хранения данных, подсистему постобработки и представления данных.
Методика разработки. Математическая модель кинематики двуногой ходьбы представляет собой ряд аналитических зависимостей, которые строятся на основе исследований в области биомеханики [1]. Исходными данными являются: масс-инерционные характеристики (МИХ) сегментов тела человека, скорость ходьбы, длина шага, уравнения, описывающие движение в суставах.
Двуногий антропоморфный механизм – это механико-математическая модель, отражающая основные динамические особенности естественных двуногих существ, в частности, человека [2]. Рассмотрим пространственный 21-звенный механизм, моделирующий скелет человека. Число степеней свободы живого организма намного превышает то, с чем имеет дело теория механизмов и машин. Поэтому разделим модель скелета человека на конечное число звеньев, что позволит упросить задачу расчета [3]. Звено 0 моделирует таз; 1, 5 – бедра; 2, 6 – голени; 3, 7 – стопы; 4, 8 – пальцы ног; 9 – нижнюю часть туловища; 10 – среднюю часть туловища; 11 – верхнюю часть туловища; 12, 15 – плечи; 13, 16 – предплечья; 14, 17 – кисти; 18 – шею; 19 – голову; 20 звено – нижнюю челюсть. В нашей модели некоторые звенья будут объединены, так как не рассматривается их движение относительно других (например, головы относительно шеи). Производим объединение звеньев «шея» и «нижняя челюсть» сегментом «голова», звено «пальцы ног» включаем в сегмент «стопа».
В представленной модели соединения считаются голономными, стационарными и удерживающими. Последнее условие означает, что звенья сочленяются без зазоров, а элементы кинематических пар не деформируются [4]. Звенья являются абсолютно твердыми телами.
Суставы моделируются шарнирами в трёхмерной системе координат (СК). Каждый сустав поставлен в соответствие одному из звеньев, и в каждом суставе можно вычислить кинематические и динамические характеристики в проекциях на оси абсолютной СК.
На рис. 1 изображена схема плоской модели двуногого устройства. При исходном положении модели ось NZ системы координат NXYZ в каждом суставе параллельна сагиттальной анатомической оси, ось NY параллельна продольной анатомической оси, а ось NX параллельна фронтальной анатомической оси. Оси абсолютной СК имеют одинаковое направление с осями локальных СК при исходном положении модели, когда все углы в суставах равны нулю. Абсолютную СК связываем с платформой, по которой будет происходить движение, это левосторонняя декартовая инерциальная СК с тремя измерениями. Каждая i-я локальная СК, где i – номер звена, представляет собой ортогональную СК и связана с проксимальным суставом i-го звена [5].
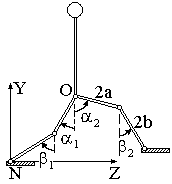
Рис. 1. Условная схема двуногого устройства.
При решении прямой задачи динамики считается, что известны законы движения всех звеньев (обобщенные координаты), и определяются суставные моменты и динамические нагрузки в суставах. Расчет позволяет оценить прочность и надежность системы [1]. Составим уравнения для расчета сил реакции в кинематических парах рассматриваемого механизма (рис. 1). Для этого воспользуемся уравнением Лагранжа второго рода [6]:
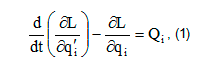
где L=K - П – функция Лагранжа, K – кинетическая энергия, П – потенциальная энергия, Qi – обобщенная сила ; qi, qi’ – соответственно обобщенные координата и скорость.
Для решения прямой задачи динамики требуется формализовать кинематику ОДА, синтезировать аналитические зависимости, описывающие движение в суставах ОДА; затем необходимо на основе данных биомеханики (МИХ сегментов) рассчитать кинетическую и потенциальную энергии в сегментах тела и продифференцировать их в уравнении (1) Лагранжа.
Рассмотрим ходьбу как сложное циклическое локомоторное действие, одним из основных элементов которого является шаг. В шагательных движениях каждая нога поочередно бывает опорной и переносной. Рассматриваем такое ритмичное движение аппарата, при котором конфигурация «двуногого» устройства повторяется с некоторым периодом T [2]. Параметры походки исследуем при среднем темпе ходьбы человека.
Считаем, что стопа отсутствует и контакт ноги с поверхностью – точечный. Пусть (zv; yv) – координаты точки опоры, где v – индекс опорной ноги, равен единице (рис. 1); (z0; y0) – координаты точки O подвеса ног. Тогда имеем зависимости:
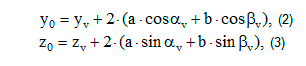
где a – половина длины бедра, b – половина длины голени, αv – угол поворота бедра опорной ноги, βv – угол поворота голени опорной ноги.
Считаем, что координаты точки O и координаты «пятки» ноги (yv; zv) заданы. Причем для опорной ноги координаты (yv; zv) – это координаты точки опоры; для переносной ноги это некоторые функции времени.
Для расчета обобщенных координат системы необходимо вычислить углы в суставах. Углы в суставах ног в случае a¹b определяются так [2]:
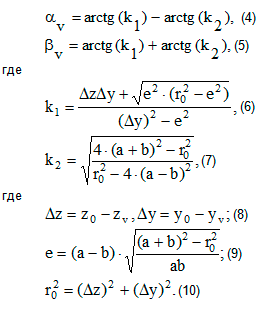
В уравнении (1) и при расчете кинетической энергии звена используются первые и вторые производные обобщенной координаты – скорость и ускорение звена. Определяем угловые скорости для тазобедренного и коленного суставов:
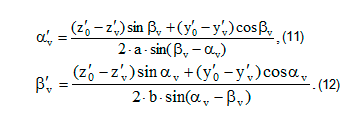
Угловые ускорения в тазобедренном и коленном суставах –αv”, βv” – получаем дифференцированием уравнений (11), (12) по времени.
Таким образом, для определения суставных углов бедра и голени необходимо лишь задать координаты точки подвеса ноги и координаты точки опоры («пятки») ноги. Точкой подвеса для каждой ноги в пространственной модели считаем тазобедренный сустав. Положение тазобедренного сустава определяется из координат таза в абсолютной СК.
Центр тяжести тела при ходьбе наряду с поступательными движениями (вперед), совершает движения боковые и в вертикальном направлении. В последнем случае размах (вверх и вниз) достигает величины 40 мм (у взрослого человека). Боковые движения (качания в стороны) центра тяжести доходят до 20 мм [1]. Точка О движется равномерно вдоль оси NZ.
Зададим движение точки O (x0; y0; z0) подвеса ног:
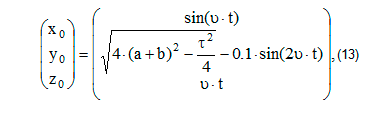
где τ – длина шага, υ – скорость ходьбы, t – номер кадра.
Для определения углов в суставах ног задаем координаты стоп. Так как рассматривается периодическое движение, то координаты стоп при задаются так:
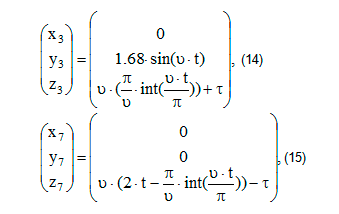
где (x3; y3; z3) – координаты стопы правой ноги, (x7; y7; z7) – координаты стопы левой ноги.
Движение стоп при sin(υ·t)≤0 задается уравнениями (16), (17):
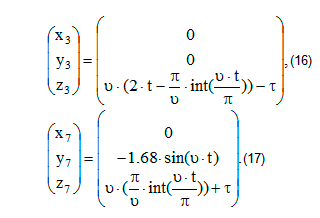
Углы стоп и пальцев ног равны нулю во всех проекциях на абсолютную СК, так как рассматривается бесстопная модель, то есть стопа не вращается относительно абсолютной СК. Углы поворота в правом и левом плечевых суставах соответственно:
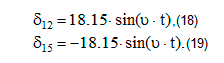
Углы поворота в правом и левом локтевых суставах соответственно:
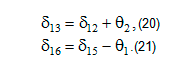
Руки двигаются по периодическому закону, то есть при sin(υ·t)>0:
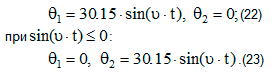
Уравнения изменения углов кистей такие же, как в уравнениях (20), (21), так как кисти при ходьбе не вращаются относительно предплечий.
Пространственная модель ходьбы включает в себя также движение тела человека (туловища) во фронтальной плоскости. Таким образом, имеем уравнение изменения угла наклона нижней части туловища в плоскости XNY, которое используется для вычисления движения остального тела:
![]()
где – угол поворота нижней части туловища в плоскости XNY.
Определим линейные составляющие обобщенных координат. Для этого по заданным значениям углов определяем начальные позиции дистальных костей [3]:
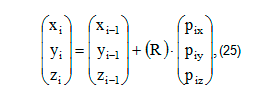
где (xi; yi; zi) – координаты текущей кости, (xi-1; yi-1; zi-1) – координаты предыдущей в иерархии кости, R – матрица трансформации, (px; py; pz) – проекции кости на оси локальной СК (при исходном положении тела).
Матрица трансформации размерностью [3´3] в общем случае представляет собой произведение матриц поворота вокруг осей NX, NY и NZ.
Составляющие мгновенных угловых и линейных скоростей для суставов определяются дифференцированием функций их углов и абсолютных координат. Угловые и линейные ускорения определяются дифференцированием выражений для угловых и линейных скоростей [6].
При построении динамической расчетной схемы антропоморфного механизма необходимо знать МИХ сегментов тела человека, то есть массу, моменты инерции, координаты центров масс сегментов тела. Один из косвенных методов определения МИХ – это определение по уравнениям регрессии, в которых аргументами являются вес (X1) и длина (X2) тела [5]:
Y = B0+B1X1+B2X2,(26)
где B0, B1, B2 – коэффициенты уравнения множественной регрессии.
Значения коэффициентов для определения моментов инерции, а также для определения масс сегментов приведены в [1]. Координаты положения центров масс сегментов на их продольных осях определяются в процентах к длинам сегментов [1].
Определив потенциальные и кинетические энергии сегментов модели, продифференцируем их по времени и получим выражения для расчета обобщенных сил в кинематических парах механизма.
Анимация движения выполняется с использованием графической библиотеки OpenGL для программирования компьютерной графики. Для каждого сегмента ОДА разработана полигональная модель в пакете 3D Studio Max. Способ взаимодействия сегментов ОДА детерминирован математической моделью.
Проблема хранения параметров модели и результатов эксперимента решается с помощью базы данных. В качестве СУБД выбран сервер PostgreSQL, поскольку это открытый продукт, основанный на клиент-серверной технологии, а его возможности обработки транзакций, многоверсионность и объектно-реляционная архитектура создают преимущества перед аналогичными серверами MySQL, FirebirdSQL. Логическая модель базы данных представлена на рис. 2.
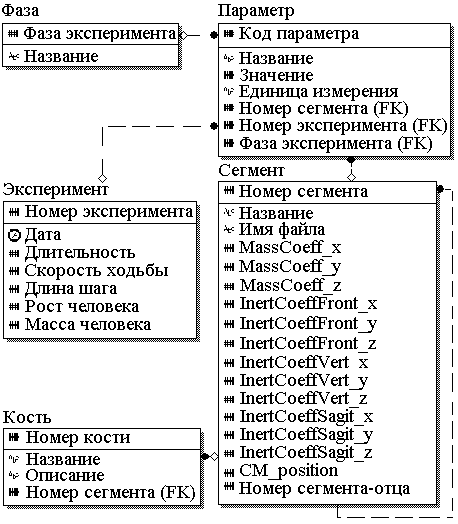
Рис. 2. Логическая модель базы данных.
Все параметры модели, динамически изменяющиеся в ходе вычислительного эксперимента, представлены в виде графиков и таблиц, в которых отражены компоненты векторов, их длины, минимальные и максимальные значения параметров за весь цикл ходьбы. Есть возможность экспорта табличных данных в html-код, графических данных – в bmp-формат.
Экспериментальная часть. Разработана программа, которая производит вычисление величин сил в кинематических парах модели на основе предложенных аналитических зависимостей. Вычисление сил происходит в режиме реального времени. Экранная форма программы представлена на рис. 3.
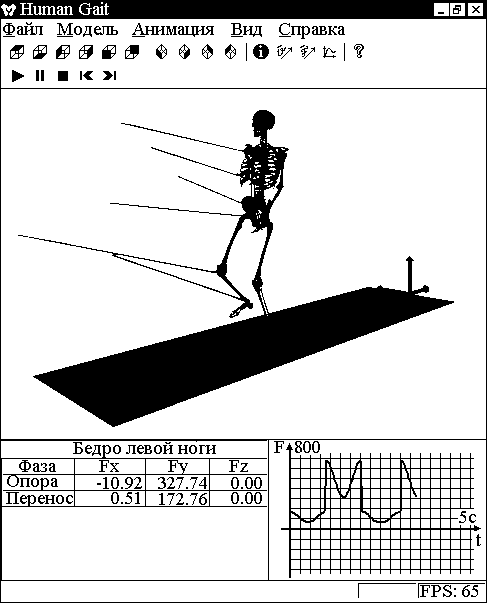
Рис. 3. Экранная форма программы.
Одним из приложений расчетов является анализ стабильности фиксирующих устройств для таза, при котором необходимо знать значения сил, действующих на таз в динамике при различных видах локомоций. В результате вычислительного эксперимента, в частности, было получены значения силы в головке бедренной кости для человека ростом 1.76 м и массой 65 кг при скорости ходьбы 1.2 м/с (табл. 1).
Таблица 1. Значения сил в тазобедренном суставе левой ноги
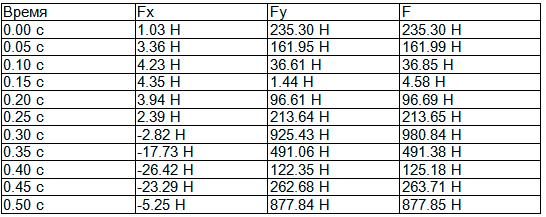
Получены максимальные значения силы в тазобедренном суставе при скорости 1.2 м/с: 1) 1074 Н – для человека ростом 1.76 м и массой 70 кг; 2) 980 H – для человека ростом 1.76 м и массой 65 кг.
В качестве нагрузки, действующей в тазобедренном суставе, в [7-12] рассматривается сила, статически приложенная к головке или шейке бедренной кости. Данные по ее величине обобщены в табл. 2.
Таблица 2. Значения силы P, действующей на головку бедренной кости
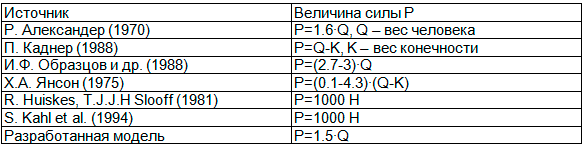
Результаты расчетов по разработанной методике определения сил, возникающих в ОДА человека при заданном варианте нагружения, аналогичны экспериментальным данным, приводимым в литературе.
В работе получены следующие результаты:
– модель антропоморфного механизма, учитывающая особенности конкретного человека, такие как: МИХ, скорость ходьбы и длину шага;
– кинематические соотношения для описания движения 21-звенной системы; методика определения нагрузок, возникающих в суставах ОДА человека при локомоторных движениях;
– специализированная ИАС, включающая в себя базу данных для хранения информации об элементах математической модели и результатах вычислительного эксперимента;
– получено авторское свидетельство [13] на программный продукт. Анализ полученных данных позволит проводить исследования по созданию фиксирующих устройств для лечения переломов длинных костей и костей таза.
