Введение. В настоящее время одна из основных задач медицинской науки и практики заключается в построении гибких программ лечения инфекционных заболеваний на основе усиления иммунного ответа. В связи с этим представляют интерес задачи стимуляции иммунного ответа при инфекционных заболеваниях, где стимуляция основана на возможных фармакологических или физиологических воздействиях на организм с целью лечения заболевания. Наибольшую сложность при лечении представляют хронические формы заболеваний. Поэтому актуальны постановка и решение задач усиления иммунного ответа при хронических формах болезни.
Базовая модель инфекционного заболевания. Наиболее общие закономерности иммунной защиты организма при инфекционных заболеваниях отражены в базовой математической модели инфекционного заболевания, предложенной Г.И. Марчуком [4]. В рамках модели стимуляция иммунной системы может быть отражена введением управляющих функций, характеризующих внешние воздействия на иммунный ответ. В качестве механизма стимуляции будем рассматривать иммунотерапию, основанную на введении готовых иммуноглобулинов или донорских антител. Модификация базовой модели с учётом управления имеет вид [2]
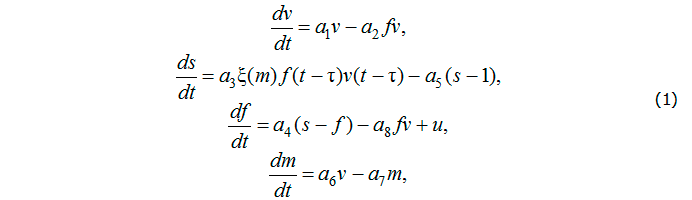
где v, s, f – соответственно относительные концентрации антигенов, плазматических клеток и антител, m – доля разрушенных антигенами клеток. Параметры модели 
характеризуют иммунный статус организма и свойства антигена, τ – время, необходимое для формирования каскада плазматических клеток. Непрерывная невозрастающая неотрицательная функция 
, учитывающая нарушение нормальной работы иммунной системы вследствие существенного поражения органа, может быть представлена следующим образом:
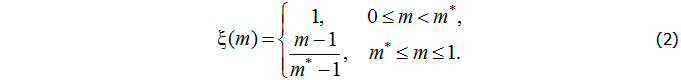
Начальные условия, характеризующие наличие устойчивой хронической формы заболевания, имеют вид [1]
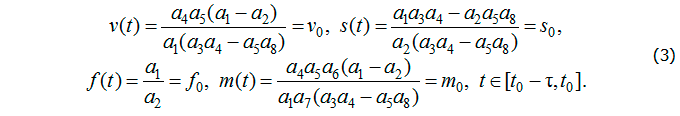
В силу автономности системы (1) за начальный момент примем 
. Будем считать, что клинико-лабораторные показатели можно получить в определенные моменты времени, соответствующие узлам сетки
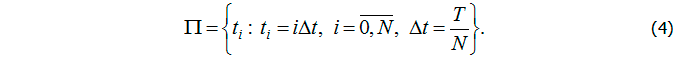
Управляющая функция характеризует скорость введения готовых иммуноглобулинов или донорских антител. Будем рассматривать два способа построения управления.
- Непрерывное введение донорских антител в течение равных промежутков времени, что на практике соответствует поступлению препаратов через капельницу. В этом случае управляющая функция выбирается из множества
- Дискретное введение донорских антител через равные промежутки времени, что на практике соответствует инъекциям лекарственных препаратов:
где δ(t) – дельта-функция.
Ограничение B > 0 учитывает физиологически допустимые дозы применения препаратов.
Построение управления иммунным ответом в условиях с неполной информацией.
Вначале сформулируем цель управления иммунным ответом при хронической форме заболевания:
что соответствует выздоровлению, то есть переходу из устойчивой хронической формы в состояние здорового организма.
Для решения поставленной задачи рассмотрим стационарное решение базовой модели инфекционного заболевания с управлением:
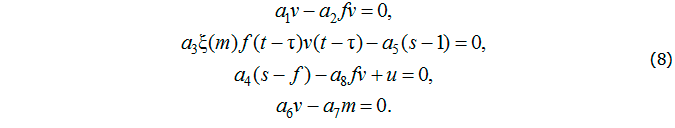
Из первого уравнения получим
откуда следует соотношение для концентрации антител
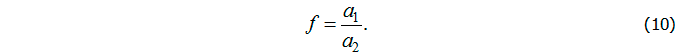
Учитывая, что управление должно обеспечить равенство концентрации антигенов нулю (v = 0), из второго уравнения получим s = 1. Тогда из третьего уравнения следует соотношение для управляющей функции:
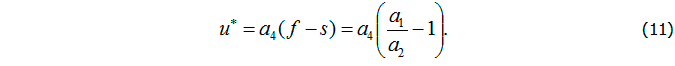
Хроническая форма заболевания может характеризоваться следующим набором параметров [4]:
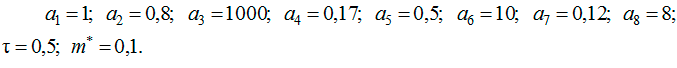
При данных значениях параметров получим 
Поскольку параметры модели характеризуют иммунный статус организма, зная значения параметров, можно построить программу лечения для конкретного пациента. Однако в реальных условиях параметры системы не известны, поэтому необходимо использовать методы, позволяющие строить управление в условиях с неполной информацией, когда значения параметров неизвестны, а их оценка корректируется по мере поступления новых клинических данных.
Рассмотрим методику, позволяющую строить программу лечения в процессе измерения клинических показателей. Предлагаемый подход представляет собой модификацию метода, сформулированного в работе [6], основная идея которого заключается в том, что фазовую траекторию концентрации антигенов необходимо вывести на желаемое состояние. Считается, что желаемому состоянию соответствует некоторое решение базовой модели инфекционного заболевания, которое названо опорным.
Методика построения программы лечения заключается в следующем. Сначала определяется множество фазовых переменных, значения которых можно измерить, и задаются величины допустимого отклонения расчетных значений от клинических данных.
Для каждого параметра выбирается диапазон допустимых значений:
,
где L – количество параметров. Затем случайным образом задается K наборов значений параметров.
В работе [8] показано, что для оценки параметров модели данного типа достаточно наблюдений за динамикой одной фазовой переменной. Протекание той или иной формы заболевания в рамках модели связано с динамикой антигенов. Поэтому для оценки параметров будем использовать показатели концентрации антигенов.
При 
определяются допустимые наборы параметров, то есть удовлетворяющие критерию
где ε – величина допустимого отклонения расчетных значений концентрации антигенов от лабораторных показателей, К i – количество наборов параметров в момент ti, 
Таким образом, после измерения значений фазовых переменных при t = ti необходимо найти Ki решений задачи (1) – (3) на отрезке [0, ti] , i = 0, …, N, и определить допустимые наборы параметров. В качестве оценки параметров при t = ti выбирается среднее значение допустимых наборов:
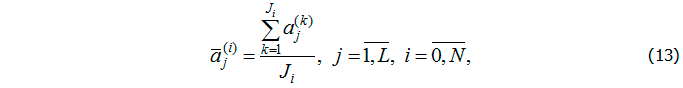
где Ji – количество допустимых наборов значений параметров в момент времени ti; , i = 0, …, N; , i = 1, …, N; , где K – первоначальное количество наборов параметров; , i = 0, …, N, где – количество неприемлемых наборов параметров в точке .
В качестве опорного решения будем задавать убывающую часть траектории из решения задачи со значениями параметров, соответствующими острой форме заболевания [7]: