При анализе данных популяционных исследований в клинической эпидемиологии наиболее часто используются изменения средних величин изучаемых показателей в комплексе с их средними ошибками (или дисперсиями) [1]. Тем не менее, было бы полезно также оценивать более ”тонкие” и универсальные изменения популяционных показателей, оценивающих колеблемость и взаимозависимость всех вариант динамического ряда как отдельного изучаемого параметра (например, уровня общего холестерина, артериального давления и др.), так и всей системы в целом.
Одно из перспективных направлений моделирования сложных медико-биологических систем, анализа эффективности проводимых медицинских интервенционных вмешательств на популяционном уровне основано на использовании энтропии. Энтропия является фундаментальным свойством любых систем с неоднозначным, или вероятностным поведением [2]. Известно, что любые объекты и явления живой и неживой природы без исключения содержат черты порядка и беспорядка, определенности и неопределенности, организованности и дезорганизованности, и, следовательно, и энтропии. Также многие показатели эффективности систем сводятся к минимизации или максимизации энтропии. Изменение энтропии зависит с одной стороны от изменения дисперсий, с другой стороны, от изменения коррелированности случайных величин. Нам представляется интересным и перспективным применить методы энтропийно-вероятностного моделирования стохастических систем в комплексной оценке динамики факторов риска (ФР) сердечно-сосудистых заболеваний в организованной популяции.
Цель исследования. Применить метод энтропийно-динамического моделирования для анализа динамики средних уровней основных измеримых факторов риска сердечно-сосудистых заболеваний во взаимосвязи с изменением общепопуляционной энтропии (включающей в себя все факторы риска) и “индивидуальной” энтропии каждого изучаемого фактора риска.
Материал и методы исследования. Данное исследование проведено в организованном коллективе работников одного из предприятий металлургической промышленности г. Челябинска. Комплексные профилактические обследования проводились в период с ноября по май 1993-1994 г., 1994-1999 г. и 2009-2010 г. Далее будет указан только год окончания профилактических осмотров. Всего было обследовано 2566 человек в возрасте от 18 до 64 лет. Характеристика по полу, возрасту, а также средний возраст обследованной популяции представлены в табл. 1. Обследовались работники одних и тех же цехов и профессий, которые в соответствии с ведомственными и внутризаводскими инструкциями подлежали ежегодному профилактическому осмотру. Было обследовано в 1994 г. 86 % от списочного состава лиц, подлежащих профилактическому осмотру, в 1999 г. – 90%, в 2010 – 88%. Сравниваемые популяции были сопоставимы по возрастно-половому составу, характеру трудовой деятельности. Оценивалась динамика таких ФР, как систолическое артериальное давление (САД), диастолическое артериальное давление (ДАД), индекс массы тела (ИМТ), уровень общего холестерина (ОХС). ИМТ определяли по формуле: ИМТ = масса тела (кг)/рост (м)². АД измерялось на правой руке в положении сидя дважды после пятиминутного отдыха в соответствии с рекомендациями протокола CINDI [3]. Уровень АД оценивался по среднему значению из двух измерений. В случае впервые выявленного повышенного АД, повторное измерение проводилось в течение 1-2 недель.
Дизайн исследования: поперечное обследование организованных популяций на рабочих местах.
В основе энтропийно-динамического моделирования лежат следующие идеи:
1. Факторный анализ показателей, в результате которого происходит деление исследуемой системы на подсистемы. Это позволяет всесторонне проанализировать исследуемый объект (систему), а также определить какие факторы (подсистемы) повлияли на изменение самого объекта (системы).
2. Для формирования динамики могут быть использованы как временные характеристики (день, месяц, год и т.п.), так и разбиение произвольного количества данных на группы испытуемых.
Для вычисления динамики энтропии будем использовать [4]:
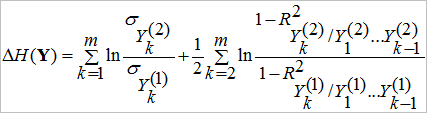 (1)
(1)
где ![]() - среднеквадратическое отклонение величин
- среднеквадратическое отклонение величин ![]() и
и 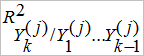 - коэффициенты детерминации соответствующих регрессионных зависимостей,
- коэффициенты детерминации соответствующих регрессионных зависимостей, ![]() ,
, ![]() .
.
Обозначим
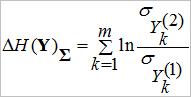 ,
, 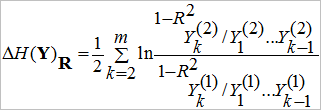 ,
,
представим формулу (1) как
![]() , (2)
, (2)
где ![]() ,
, ![]() - приращения энтропии за счет изменений дисперсий и корреляций случайных величин
- приращения энтропии за счет изменений дисперсий и корреляций случайных величин![]() [4].
[4].
Формула (2) показывает, что изменение энтропии происходит аддитивным образом, с одной стороны, за счет изменения дисперсий, а, с другой стороны, из-за изменения коррелированности случайных величин (подсистем) ![]() . Иными словами изменение энтропии носит дуальный характер. Первое слагаемое в (2) отражает изменение неопределенности системы (через сумму логарифмированных отношений среднеквадратических отклонений), а второе – изменение ее определенности (посредством анализа коррелированности между элементами системы). При увеличении слагаемого
. Иными словами изменение энтропии носит дуальный характер. Первое слагаемое в (2) отражает изменение неопределенности системы (через сумму логарифмированных отношений среднеквадратических отклонений), а второе – изменение ее определенности (посредством анализа коррелированности между элементами системы). При увеличении слагаемого ![]() энтропия
энтропия ![]() увеличивается, при увеличении слагаемого
увеличивается, при увеличении слагаемого ![]() энтропия
энтропия ![]() уменьшается.
уменьшается.
Следовательно, в результате использования энтропийно-динамической модели получается комплексный анализ всех элементов, включающий в себя основные статистические характеристики.
Таблица 1. Характеристика популяции по полу и возрасту в зависимости от года обследования
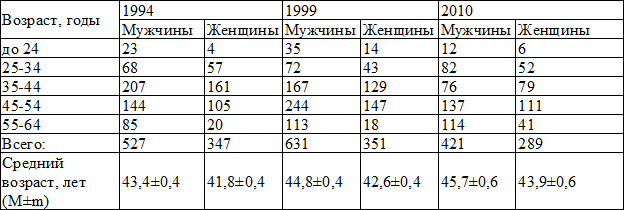
Примечание: здесь и далее M – средняя величина; m – средняя ошибка средней величины; P – уровень значимости
Полученное в результате исследования изменение энтропии можно описать следующим образом:
![]() - в течение периода происходящие в системе изменения не привели к улучшению организованности. Это могло произойти по двум причинам:
- в течение периода происходящие в системе изменения не привели к улучшению организованности. Это могло произойти по двум причинам:
1) данные по показателям не стали более упорядоченными ![]() ;
;
2) уменьшилась степень взаимодействия между элементами системы ![]() .
.
![]() - в течение периода в системе не произошло никаких изменений: (
- в течение периода в системе не произошло никаких изменений: (![]() и
и ![]() );
);
![]() - в течение периода происходящие в системе изменения привели к улучшению организованности:
- в течение периода происходящие в системе изменения привели к улучшению организованности:
1) данные по показателям стали более упорядоченными ![]() ;
;
2) увеличилась степень взаимодействия между элементами системы ![]() .
.
Статистическая обработка результатов исследования проведена на персональном компьютере с использованием программ Microsoft Access, Excel. Применялись стандартные методы вариационной статистики. Достоверность различий оценивалась с помощью параметрических методов (в основном с помощью t-критерия Стьюдента). Вычисление динамики энтропии проведено с помощью комплекса программ на языке программирования VBA Office 2007 – модуль «Вычисление эмпирического корреляционного отношения», а также на языке программирования Delphi – модуль «Вычисление динамики энтропии». Факторный анализ проведен с помощью программы STATISTICA.
Результаты исследования. Динамика средних уровней ОХС, САД, ДАД, ИМТ у мужчин и женщин представлена в табл. 2 и 3 соответственно. В мужской популяции при каждом обследовании произошло существенное снижение среднего уровня ОХС; средние уровни САД, ДАД, ИМТ в 1999 г. относительно 1994 г. не изменились, а в 2010 г. относительно 1999 г. повысились. В женской популяции при каждом обследовании произошло существенное снижение среднего уровня ОХС (изменения аналогичны изменениям в мужской популяции); средние уровни САД, ДАД в 1999 г. относительно 1994 г. снизились, а в 2010 г. относительно 1999 г. повысились до уровня первичного обследования. Средние уровни ИМТ во все годы наблюдений оставались на одном уровне.
Таким образом, популяционные изменения в распространенности основных измеримых факторов риска ССЗ носят неоднозначный и разнонаправленный характер. Для более точной и комплексной оценки динамики популяционных изменений используем метод энтропийно-динамического моделирования. Для оценки предоставлены данные по ОХС, ИМТ, САД и ДАД. На предварительном этапе проведем процедуру факторного анализа для выделения значимых ФР.
Таблица 2. Динамика средних уровней факторов риска ССЗ в популяции мужчин (M±m)

Таблица 3. Динамика средних уровней факторов риска ССЗ в популяции женщин (M±m)

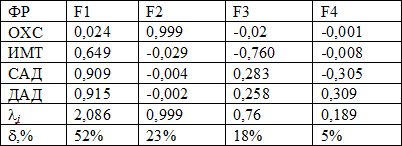
На основе факторного анализа было установлено, что исходная система может быть представлена в виде трех факторов (главных компонент), которые объясняют 93% всей вариации исходных признаков ОХС, ИМТ, САД, ДАД. Матрица факторного отображения приведена в табл. 4.
Компонента F1 характеризует артериальное давление (АД), связывающее САД и ДАД. Компонента F2 характеризует уровень ОХС и компонента F3 характеризует ИМТ. Таким образом, размерность системы сократилась с 4 до 3. В результате получили описание системы, устойчивое к вариации исходной системы входных показателей:
![]()
Таблица 4. Данные многофакторного анализа для мужской и женской популяций за все годы исследований.
Для формирования динамики будем использовать разбиение на следующие периоды: 1 период 1994 г. – 1999 г.; 2 период 1999 г.– 2010 г.
Проведем энтропийно-динамический анализ динамики ФР в мужской популяции. Динамика энтропии АД, ОХС, ИМТ для мужской популяции представлена на рис. 1. Достоверное снижение уровня ОХС в каждом периоде сопровождалось уменьшением энтропии (значения ниже 0), т.е. снизился и средний уровень ОХС, и система стала более упорядоченной по разбросу отдельных значений. По ИМТ и АД наблюдается обратная картина. По уровню АД в первый период средние уровни не изменяются, но энтропия в положительном ”поле”, т.е. колебания системы увеличиваются, во второй период увеличиваются средние уровни АД, а энтропия уменьшается и становится отрицательной, т.е. по АД система стабилизируется, становится более упорядоченной с меньшим разбросом данных на более высоких цифрах АД. По уровню ИМТ в первый период средние уровни не меняются, энтропия немного выше 0, во второй период увеличиваются средние уровни и энтропия, т.е. система становится менее организованной. Необходимо более детально анализировать динамический ряд ИМТ. Энтропийный анализ показывает, что, возможно, увеличение ИМТ произошло за счет доли лиц с высоким ИМТ, а не в целом всего ряда, о чем, кстати, косвенно свидетельствует увеличение средней ошибки средней величины.
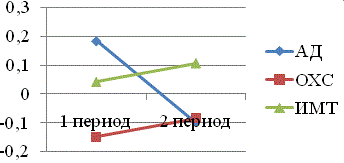
Рис. 1. Динамика энтропии уровней АД, ОХС, ИМТ для мужской популяции
Динамика комплексной энтропии по всем трем ФР представлена на рис. 3. В мужской популяции общая энтропия для всех ФР (см. рис. 3) в первый период (1994-1999 г.) была несколько выше 0, т.е. за истекший период система не стала более упорядоченной по распределению и взаимозависимости вариант, а во второй период – стала отрицательной, т.е. стабилизировалась. Проводя параллельно анализ достоверности изменений средних величин ФР, можно сделать предварительный вывод о стабилизации всей системы к 2010 г. на более “плохом” уровне (за счет ухудшения показателей по АД и ИМТ, несмотря на положительную динамику уровня ОХС). Однако требуются дальнейшие исследования для построения точной модели комплексной оценки общей для всех ФР энтропии во взаимосвязи со средними величинами.
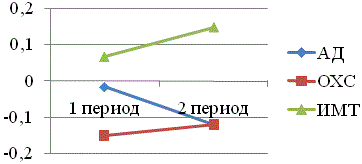
Рис. 2. Динамика энтропии уровней АД, ОХС, ИМТ для женской популяции
В женской популяции изменения энтропии (см. рис. 2) и средних уровней ОХС были аналогичны изменениям в мужской популяции. Средние значения ИМТ не изменялись, однако энтропия росла в положительных значениях, т.е. система становилась менее организованной, с большим разбросом вариант, особенно во второй период, что косвенно может свидетельствовать о неблагоприятных тенденциях. По АД в первый период наблюдались благоприятные изменения – существенное снижение среднего уровня при нулевом уровне энтропии, в то время как во второй период произошел отрицательный сдвиг системы по АД – средний уровень вырос одновременно с существенным снижением энтропии, т.е. АД равномерно, стабильно повысилось во всей популяции.
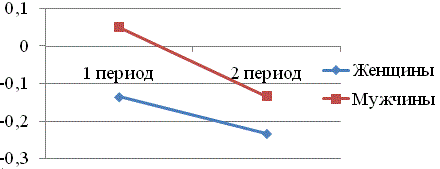
Рис. 3. Динамика комплексной энтропии для мужской и женской популяции
Таким образом, дополнительное к методу оценки популяционных изменений по средним величинам использование энтропийно-динамической модели имеет следующие преимущества:
1. Энтропийно-динамическая модель позволяет исследовать систему комплексно. Результаты могут быть получены как по отдельным элементам системы, так и по всей системе в целом, что практически невозможно сделать при количественной оценке отдельных показателей системы.
2. Энтропийно-динамическая модель хотя и не показывает количественное изменение исследуемых параметров, но дает более глубокую оценку сущности этого изменения. Например, если известно, что какое-либо среднее значение количественного показателя понизилось, то с помощью энтропийно-динамической модели можно ответить, было ли это понижение равномерным и организованным. Поэтому для более полной оценки изменений популяционных параметров целесообразно проведение энтропийно-динамического анализа в дополнение к существующим методам.
3. Энтропийно-динамическая модель также может успешно применяться при проверке корректности исходных (вводных) данных. Если происходит существенный рост энтропии в положительных значениях, особенно при небольшой разнице в средних величинах, необходимо проверить динамический ряд на предмет исключения случайных и систематических ошибок.
Вывод. Использование энтропийно-динамической модели в дополнение к оценке популяционных изменений по средним величинам целесообразно и позволяет проводить более глубокий анализ динамики изучаемых параметров состояния здоровья населения.
