Задача постановки диагноза по имеющемуся набору симптомов заболевания у больного достаточно сложна и носит многокритериальный характер. Осматривая больного, выслушивая его жалобы и выявляя значимые симптомы, врач при каждом приеме принимает решение, основываясь на своих знаниях и опыте. Ограничение выбора решения в таком процессе конечным множеством предполагаемых диагнозов позволяет снизить вероятность ошибки постановки предварительного диагноза. В данной статье рассматривается вариант реализации автоматизированного процесса построения конечного множества предложений для врача при помощи медицинской информационной системы поддержки принятия решений на основе использования правил Байеса.
Байесовские сети доверия (Bayesian Belief Network) используются в тех областях, которые характеризуются наследованной неопределённостью. Эта неопределённость может возникать вследствие:
- неполного понимания предметной области;
- неполных знаний;
- когда задача характеризуется случайностью.
Для Байесовских сетей доверия иногда используется ещё одно название – причинно-следственная сеть, т.е. сеть, в которой случайные события соединены причинно-следственными связями.
Для представления неопределенности знаний можно весьма эффективно использовать положения теории вероятностей. Подобные представления базируются на понятии условной вероятности – вероятности наступления события d при наступившем событии s. Например, условной вероятностью является вероятность того, что у пациента имеется заболевание d, если у него обнаружен симптом s. Для вычисления условной вероятности используется следующая формула:
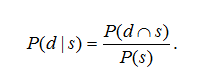
Как видно из данной формулы, условная вероятность определяется через понятие совместности или одновременности событий, то есть вероятности совпадения событий d и s, разделенная на вероятность события s. Очевидно, что вероятность совпадения или произведения двух событий равна произведению вероятности одного из них и условной вероятности другого, вычисленную при условии, что первое имело место:
P(d∩s)=P(s).P(d/s) или P(d∩s)=P(d).P(s/d).
Подставляя последнее выражение в формулу, соответствующую определению условной вероятности, можно получить правило Байеса в простейшем виде:
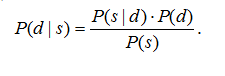
Это правило позволяет определить вероятность P(d | s) появления события d при условии, что произошло событие s через заранее известную условную вероятность P(s | d). В полученном выражении P(d) – априорная вероятность наступления события d, а P(d | s) – вероятность того, что событие d произойдет, если известно, что событие s свершилось. Данное правило иногда называют инверсной формулой для условной вероятности, так как она позволяет вычислить вероятность P(d | s) через P(s | d).
На практике нам необходимы распределения интересующих нас пере-менных, взятые по отдельности. Они могут быть получены из соотношения для полной вероятности при помощи маргинализации – суммирования по реализациям всех переменных, кроме выбранных.
Рассмотрим задачу моделирования выдачи диагноза на примере. Для простоты рассуждений введем следующие обозначения переменных в Байесовской сети:
R – была ли эпидемия (наличие вируса ОРВИ);
S – холодное время года;
C – инфицировано ли детское учреждение;
W – инфицировано ли студенческое общежитие.
Все четыре переменные принимают булевы значения 0 – ложь (f) или 1 – истина (t). Совместная вероятность P(R, S, C, W) да¬ется совокупной таблицей. Таблица вероятностей нормирована, так что
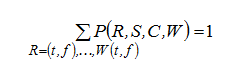
Зная совместное распределение, легко найти любые интересующие нас условные и частичные распределения. Например, вероятность того, что эпидемии не было при условии, что инфицировано студенческое общежитие вычисляется:
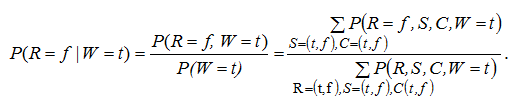
Полная вероятность в соответствии с теоремой умножения пред-ставляется цепочкой условных вероятностей:
P(R, S, C, W) = P(R) ∙ P(S) ∙ P(C |R,S) ∙ P(W | R).
Порядок следования переменных в соотношении для полной вероятности, вообще говоря, может быть любым. Однако на практике целесообразно выбирать такой порядок, при котором условные вероятности максимально редуцируются. Это происходит, если начинать с переменных-«причин», постепенно переходя к «следствиям». При этом полезно представлять себе некоторую «историю», согласно которой причины влияют на следствия.
Для систем, основанных на знаниях, правило Байеса гораздо удобнее формулы определения условной вероятности через вероятность одновременного наступления событий. В этом достаточно просто убедится. Пусть у пациента X имеется некоторый симптом S и необходимо узнать, какова вероятность того, что этот симптом является следствием заболевания Z. Для того, чтобы непосредственно вычислить P(Z | S), нужно оценить каким-либо образом, сколько человек в мире страдают этим заболеванием, и сколько человек одновременно имеют заболевание Z и симптом S. Такая информация, как правило, недоступна или отсутствует вообще.
Однако, если посмотреть на вероятность не как на объективную частотность событий при достаточно долгих независимых испытаниях, а как на субъективную оценку совместного наступления событий, то диагностика значительно упрощается. Например, врач может не знать или не иметь возможности определить, какая часть пациентов имеющих симптом S страдают от заболевания Z. Но на основании, например, собственного опыта или литературных данных, врач в состоянии оценить, у какой части пациентов имеющих заболевание Z встречается симптом S. Следовательно, можно вычислить P(S | Z) и применить инверсную формулу для условной вероятности.
Ситуация значительно усложняется, если речь пойдет о множестве симптомов и множестве заболеваний. Если необходимо вычислить условную вероятность для одного симптома из некоторого множества симптомов, то потребуется m•n + m + n вычислений, где m – количество возможных диагнозов, а n – число разнообразных симптомов.
Ситуация еще более усложнится, если включить в процесс постановки диагноза сразу несколько симптомов. Учитывая, что в медицинской диагностике используются тысячи видов заболеваний и огромное количество симптомов, эта задача становится нетривиальной. Правило Байеса в обобщенной форме выглядит следующим образом:
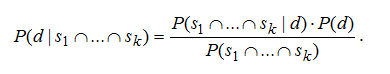
Данная формула требует (m . n)2 + m2 + n2 вычислений оценок вероятностей, что даже при небольшом k является достаточно большим числом. Такое количество оценок требуется по той причине, что для вычисления P(s1 ... ∩ sk ) в общем случае сначала требуется вычислить P(s1/s2 ∩...∩ sk ).P(s2 /s3 ∩ sk )·...·P(sk ). Однако если предположить что симптомы независимы, то количество вычислений резко снижается и становится таким же, как и в случае учета единственного симптома, так как для независимых si и sj вероятность:
P(sj ∩ sj )=P(sj)·P(sj)
Алгоритмическая модель для рассматриваемой автоматизированной экспертной системы была разработана на основе теоремы Байеса:
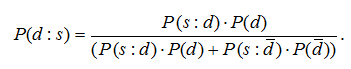
Вероятность осуществления некой гипотезы d при наличии определенных подтверждающих свидетельств s вычисляется на основе априорной вероятности этой гипотезы без подтверждающих свидетельств и вероятности осуществления свидетельств при условиях, что гипотеза верна (событие d) или неверна (событие ). Поэтому, возвращаясь к проблеме диагностики заболеваний, оказывается, что:
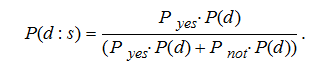
Считаем все болезни равновероятными с Р(d)=P. Программа должна задать соответствующий вопрос и, в зависимости от ответа, вычислить Р(d:s). Ответ «Да» (Pyes) подтверждает вышеуказанные расчеты, ответ «Нет» (Pnot) тоже, но с вероятностями (1 – Pyes) и (1 – Pnot) вместо Pyes и Pnot. После этого априорная вероятность Р(d) может быть заменена на Р(d:s). Затем продолжается выполнение программы, но с учетом постоянной коррекции значения Р(d) после каждого шага итерации. Общая схема алгоритма выбора диагноза представлена на рис. 1.
Алгоритм выбора диагноза можно разделить на несколько шагов:
Шаг 1. Ввод исходной информации – набора симптомов, после чего программа ищет информацию о том, сколько записано болезней с соответствующей симптоматикой в базе знаний (N – количество соответствующих симптомам болезней, n – номер рассматриваемой болезни: 0≤n≤N).
Шаг 2. Установка счетчика болезней: (исходное состояние n=0) n=n+1. Выбирается первая, а затем, последовательно, и следующая из отобранных болезней.
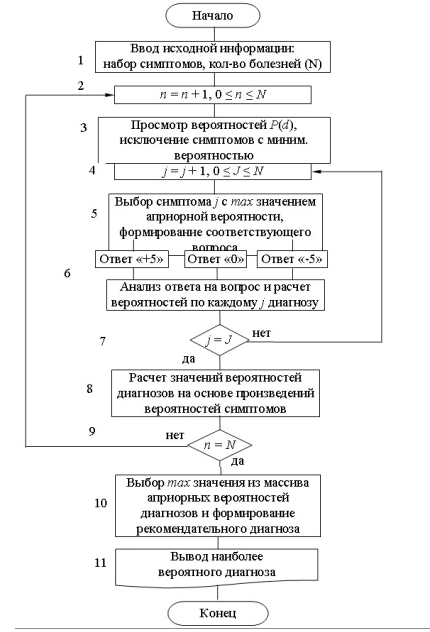
Рис. 1. Общая схема выбора диагноза
Шаг 3. Просматриваются все априорные вероятности Р(d), относящиеся к введенному набору симптомов и также к выбранной болезни. Это делается для того, чтобы определить, какие симптомы являются самыми важными, и выяснить, о чем спрашивать в первую очередь. Симптомы с минимальной вероятностью исключаются (J – количество отобранных симптомов в наборе, j – номер текущего симптома: 0≤j≤J).
Шаг 4. Установка счетчика симптомов: (исходное состояние j=0) j=j+1. Выбирается первый, а затем, последовательно, и следующий из отобранных симптомов.
Шаг 5. Выбирается симптом с самой большой вероятностью присутствия. Программа находит и задает вопрос, соответствующий этому симптому.
Шаг 6. Ответ производится по шкале от -5 до + 5, чтобы отразить степень уверенности в ответе.
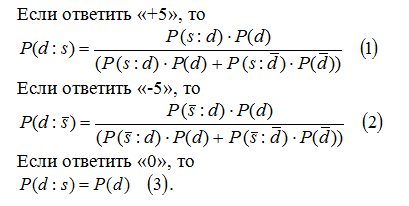
Если же значение находится в промежутках между указанными точками, то будет понемногу и того, и другого, отраженное соответствующими весовыми коэффициентами, т.е. программа вычисляет, сколько же этого «и одного», «и другого».
Шаг 7. Проверяется, все ли J симптомов рассмотрены. Если «нет», то переход к рассмотрению следующего из отобранных симптомов (за исключением уже рассмотренного), переход к шагу 4.
Шаг 8. Подсчитываются новые значения вероятностей в правилах Байеса. Определяются минимальное и максимальное значения вероятностей для каждой болезни, основанные на существующих в данный момент априорных вероятностях и предположениях, что оставшиеся свидетельства будут говорить в пользу гипотезы или противоречить ей. Важно выяснить: стоит ли данную гипотезу продолжать рассматривать или нет? Это определяется расчетом совокупной условной вероятности для всех симптомов. Гипотезы, которые не имеют смысла, просто отбрасываются. Те же из них, чьи минимальные значения выше определенного уровня, могут считаться возможными исходами, т.е. возможными болезнями и подлежат дальнейшей диагностике.
Шаг 9. Проверяется, все ли N болезней рассмотрены. Если «нет», то переход к рассмотрению очередной из отобранных болезней, т.е. переход к шагу 2. Если «да», то переход к следующему шагу.
Шаг 10. Отбор максимальной из условных вероятностей рассмотренных болезней и выбор этой болезни в качестве рекомендации по диагностике отмеченных симптомов для лечащего врача.
Шаг 11. Вывод рекомендованного диагноза.
Медицинская информационная система, реализующая рассмотренный выше алгоритм алгоритма выдает конечное множество рекомендаций врачу относительно соответствия симптомов, обозначенных пациентом, наиболее вероятным заболеваниям. В свою очередь, врач имеет возможность использовать такую медицинскую систему в качестве средства частичной автоматизации сложнейшего процесса диагностирования больного. А это позволит несколько разгрузить и упорядочить работу медработников, а также исключить полную зависимость постановки диагноза больному только от человеческого фактора и повысить степень объективности диагностики заболеваний.
