Использование законов биомеханики в совокупности с математическим моделированием дает возможность раскрыть механизм воздействия извне на живую ткань. В частности, говоря о стоматологии – это воздействие протеза на опорные зубы и костную ткань челюсти. Одна из основных проблем современной ортопедической стоматологии неразрывно связана с проектированием зубопротезных конструкций, которые обладают достаточной прочностью, легкостью и функциональностью. Изучение закономерностей биомеханических процессов, особенно механизмов передачи и распределения функциональных нагрузок на окружающие биологические ткани, не приспособленные к восприятию жевательного давления, имеет большое теоретическое и практическое значение [2-4, 6]. Костная ткань отвечает на возникшее в ней напряжение развитием напряженно-деформированного состояния опорных тканей, которое определяет процессы развития и разрушения кости. Использование компьютерной вычислительной техники позволяет создавать сложные модели разных объектов сложной конфигурации и изучать их функционирование при различных условиях. В настоящее время самым информативным методом изучения биомеханики зубочелюстной системы признан метод конечных элементов (МКЭ). В ортопедической стоматологии появились научные исследования, основанные на методе конечных элементов [9], что связано с рядом преимуществ этого метода перед натурными испытаниями, особенно в возможности оценки не только реальных ситуаций полости рта, но необычных функциональных нагрузок по величине, направлению и точке приложения.
Цель исследования: изучение распределения внутренних напряжений в костной ткани при использовании бюгельного протеза для замещения дефекта зубного ряда с потерей трех зубов в целях выбора оптимальной конструкции зубного протеза.
Материал и методы: для изучения распределения внутренних напряжений мы применили математическую модель, в основу создания которой положен метод конечных элементов. Двухмерная модель представляет собой фрагмент нижней челюсти с дефектом зубного ряда, на котором моделируется бюгельный протез. При этом изучается дефект потери трех зубов от клыка до второго моляра. Модель состоит из треугольных конечных элементов, имеющих три точки взаимодействия между собой. На модели зубы моделируются только схематично, как изотропный (однородный) материал, согласно принципу Сен-Венана. Учитывая геометрическую форму зуба при моделировании зубного протеза, определяются точки закрепления нагрузки. Для проведения исследований напряженно-деформированного состояния объекта к модели необходимо приложить нагрузки, действующие на реальный объект, а сама модель наделяется физико-механическими характеристиками, соответствующими реальному объекту. После проведения необходимых действий, выполняемых с помощью электронно-вычислительной техники, получается полная информация о распределении напряжений, деформаций и смещений в любой точке рассматриваемого объекта. При создании математической модели нами было принято важное условие функционирования модели, которое заключается в том, что зубной протез плотно прилегает к слизистой оболочке или опорным зубам, в противном случае не будет осуществляться передача напряжений с одного изучаемого объекта на другой. Для изучения влияния зубных протезов на опорные зубы и околозубные ткани построили математическую модель с дефектом зубного ряда при отсутствии первого и второго премоляра, первого моляра.
Для построения двухмерной модели выполнили следующие этапы:
1. В заданном масштабе вычертили контур модели дефекта зубного ряда от клыка до второго моляра.
2. С помощью специальной программы выполнили автоматизированное разбиение объекта на треугольные конечные элементы.
3. Осуществили задание физико-механических характеристик различных частей конечно-элементной модели в соответствии с особенностями реального объекта.
4. Осуществляли привязку сил, воздействующих на опорные зубы и слизистую оболочку.
5. Выполнили задание нагрузок на модель.
Полученная модель состоит из 932 треугольных конечных элементов, которые имеют три точки взаимодействия между собой, и насчитывают 541 узловую точку, количество точек закрепления зависит от вида протеза (рис. 1).
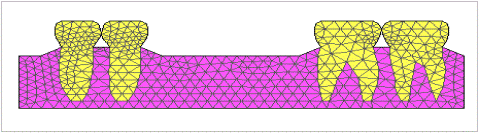
Рис. 1. Конечно-элементная модель дефекта зубного ряда.
Модель построена с учетом реальных средних размеров дефектов возникающих в полости рта при удалении двух премоляров и одного моляра и характеризуется следующими параметрами: расстояние между зубами, ограничивающими дефект 32 мм, ширина медиального зуба (клыка) – 8 мм, ширина дистального зуба (моляра) – 12 мм, длина зубов – 27 мм. Между зубами смоделирован контактный пункт, который после препарирования восстанавливается протезом, а при использовании съемных конструкций контактный пункт не нарушается.
Бюгельный протез моделируется таким образом, что жевательная нагрузка воспринимается в первую очередь опорными зубами, через опорноудерживающие кламмера по 30% на каждый зуб, и в меньшей степени протезное ложе до 40%.
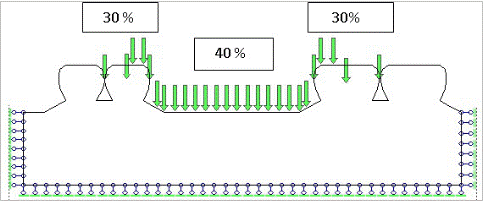
Рис. 2. Точки закрепления нагрузок при замещении дефекта зубного ряда бюгельным протезом.
Для проведения исследования распределения внутренних напряжений использовано 55 точек закрепления на модели. Нагрузка прикладывается к точкам закрепления на зубах. Под точками закрепления понимаются места приложения силы по направлению и величине, через которые осуществляется воздействие на модель, либо места контакта с каким либо объектом. Сила жевательной нагрузки определяется как 100 H на исследуемый объект, то есть нагрузка, испытываемая протезом при разжевывании пищи средней твердости.
Для изучения распределения напряжений в челюсти при использовании бюгельного протеза принимаются следующие условия функционирования модели:
- 100% плотность губчатой кости 15 · 103 кг/см2, плотность дентина 200 · 103 кг/см2 , - коэффициент Пуассона 0,30;
- нагрузка распределяется по 30 % на опорные зубы, 40 % на промежуточную часть.
Нагрузка прикладывается к точкам закрепления. Под точками закрепления понимаются места приложения силы по направлению и величине, через которые осуществляется воздействие на модель, либо места контакта с каким либо объектом. На модели изучается распределение напряжений по оси Х, оси Y, эквивалентные напряжения этих осей, величина деформации, которую может претерпевать модель под действием нагрузки (рис 2). Для описания и обсуждения результатов мы воспользовались картиной распределения эквивалентных напряжений, построением графиков распределения внутренних напряжений, согласно выбранных нами линий. В данном исследовании напряжения определялись в условных единицах.
Результаты исследования и их обсуждение. При анализе полученных результатов (рис.3) мы отмечали только положительные напряжения, так как модель подвержена растяжению. Установлено, что наибольшая концентрация внутренних напряжений находится в пришеечной области опорных зубов со стороны дефекта. В области клыка значения почти в два раз выше, чем в области второго моляра. В связи с этим в данных областях при использовании протеза возможно развитие локального пародонтита. Следует отметить, что внутренние напряжения сконцентрированы по проекции корней опорных зубов, что является наиболее физиологическим путем передачи жевательного давления. Напряжения в области дефекта зубного ряда однородны и по величине не значительны.
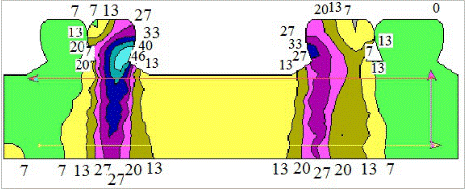
Рис. 3. Эквивалентное распределение напряжений в модели при 100% плотности костной ткани. Бюгельный протез.
На графике проведены две линии, по которым построены графики распределения напряжений. Ввиду технических особенностей построения графиков, читать результаты следующим образом. Линия, по которой вырисовываются графики, является непрерывной. Нижняя линия отражает на графике распределение внутренних напряжений по нижнему краю модели. Верхняя линия отражает на графике распределение внутренних напряжений по верхнему краю модели. Оба графика являются своеобразным срезом распределения внутренних напряжений, которые можно анализировать и сравнивать. Так как используемая линия для построения графиков является непрерывной, то верхний график является своеобразным зеркальным отображением нижнего и сравнивать их стоит именно в таком порядке. Описанные параметры построения и анализа полученных графиков будут использованы при изучении других вариантов изучения бюгельного протеза (рис. 4). Всплески повышенных напряжений располагаются в области опорных зубов воспринимающих жевательное давление. Однако следует отметить, что при распределении жевательного давления в бюгельном протезе 30% воспринимает зуб, а 20% десна, при этом соотношение зуб - сегмент альвеолярного гребня соотносятся как 1.5:1. Распределение внутренних напряжений дает следующее соотношение зуб - сегмент альвеолярного гребня как 2.2: . Таким образом, протез рационально распределяет жевательное давление, не оказывая патологического влияния на альвеолярный гребень. Растяжения в клыке в поверхностных слоях на 45% выше, чем у моляра, в области верхушки корня клыка внутренние напряжения на 13% выше, чем в области верхушек корней моляра.
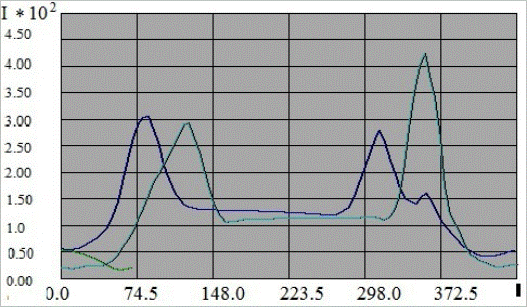
Рис. 4. График распределения внутренних напряжений в модели при восприятии нагрузки бюгельным протезом. Плотность костной ткани 100%.
Напряжения в поверхностных слоях костной ткани в области проекции клыка выше на 45%, чем у верхушки корня, напряжения в поверхностных слоях модели в области моляра на 11% выше, чем у верхушек корней. Напряжения в области дефекта зубного ряда в поверхностных слоях модели ниже на 8%, тем самым бюгельный протез защищает альвеолярную кость от атрофических процессов. Изучение распределения внутренних напряжений при 100% плотности костной ткани дало следующий результат. В поверхностных слоях модели внутренние напряжения в области клыка на 42,9 больше, чем в аналогичной области моляра. В глубоких слоях модели соотношение распределения внутренних напряжений сохраняется, однако значения в области верхушки корня клыка всего лишь на 8,8 больше, чем в области верхушек корней моляра. В сегменте клыка внутренние напряжения в поверхностных слоях на 37,3 больше, чем в глубоких слоях модели, а в сегменте моляра внутренние напряжения в поверхностных слоях на 4,6 больше, чем в глубоких. В альвеолярном гребне внутренние напряжения в глубоких слоях модели на 10,6 больше, чем в поверхностных слоях модели.
Выводы. По результатам исследования можно сделать вывод, что наиболее оптимальным видом протезирования является использование бюгельного протеза с цельнолитым базисом, который защищает опорные зубы от чрезмерной нагрузки и от возникновения заболеваний пародонта.
