Одним из неблагоприятных факторов, вызывающих серьезные заболевания, является высокий уровень холестерина в крови. Он может привести к сужению сосудов, образованию камней в желчном пузыре и другим тяжелым последствиям. Поэтому важной задачей является выявление групп риска, у которых возможно появление серьезных заболеваний на фоне высокого уровня холестерина. В данной статье на основе модельного подхода предложен критерий такого развития событий, позволяющий оценить функциональное состояние человека, и на основе статического подхода определить условия его применения.
В настоящее время с развитием информационных технологий особую актуальность приобретают неинвазивные методы исследования состояния организма человека или отдельных его органов. Как правило, они представляют собой способы автоматизированной идентификации патологий по результатам косвенных анализов и измерений без травматичного проникновения внутрь организма [1]. Особую группу составляют неинвазивные методы, основанные на использовании биосигналов, таких, например, как сигналы электрической активности сердечной мышцы или сигналы механических пульсаций кровеносных сосудов. Особенность отмеченных биосигналов заключается в том, что они несут информацию одновременно о многих параметрах организма, но в неявном виде. Кроме того, совместная обработка нескольких сигналов различного биологического и физического происхождения от разных (но связанных) подсистем организма позволяет выявить патологии на ранних стадиях, когда уже нарушены взаимосвязи систем организма (регуляторные функции), но эти нарушения еще не приобрели выраженных патологических форм.
Отличительной особенностью современных методов обработки сигналов является использование модельных представлений об объекте наблюдения. В случае биосистем основной проблемой является идентификация модели органа по порождаемому им сигналу. Поэтому задача интерпретации биосигналов представляет особую задачу идентификации сложной системы, когда необходимо не только решить задачу структурной идентификации подсистем, но и решить задачу параметрической идентификации, включая идентификацию характеристик и параметров взаимосвязей подсистем.
Традиционно в качестве характеристик взаимной связи процессов используются взаимокорреляционные функции, функции когерентности и ряд других эмпирических характеристик связи. Однако данные методы не учитывают динамику и свойства самих систем, генерирующих временные ряды. Кроме того, на фоне сильной корреляции при незначительных изменениях параметров взаимосвязей подсистем использование подобных статистических характеристик является недостаточным.
В настоящее время наиболее перспективными являются алгоритмы, основанные на идентификации или реконструкции модельных уравнений тех или иных подсистем организма [2]. Выявление и исследование управляющих параметров, входящих в состав модельных уравнений, описывающих не только состояние подсистем, но и взаимосвязей между ними, позволит идентифицировать патологии на ранних стадиях их возникновения.
Исходной информацией в методах реконструкции (обратная задача динамики) являются выходные сигналы, генерируемые биосистемой. В принципе (теоретически), достаточно реализации одного сигнала для реконструкции системы с использованием метода задержек Такенса. Если же для регистрации доступны несколько сигналов, то точность реконструкции увеличится. Например, в случае наличия двух зарегистрированных сигналов x1(t) и x2(t) вектор фазовых переменных реконструируется следующим образом:
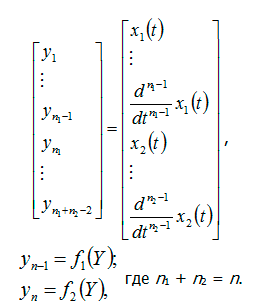
В случае полиномиальной аппроксимации функции f1(t) и f2(t) представляются в виде полиномов степени n:
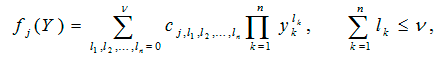
Где ![]() - неизвестные коэффициенты.
- неизвестные коэффициенты.
Однако в данном методе не учитывается априорная информация о реконструируемой системе. Универсальная форма представления реконструируемой модели не отражает особенностей функционирования систем и часто не имеет ничего общего с реальностью.
Поэтому предлагается использовать метод идентификации взаимосвязей на основе модельного представления взаимодействующих подсистем. При данном подходе подсистемы представляются базовыми моделями, построенными на основе биофизических представлений и регистрируемых биосигналов. Взаимодействие подсистем описывается традиционно правыми частями модельных уравнений, где стоят неизвестные функции взаимосвязи. В случае зарождения патологии, то есть изменения функционального состояния, организм человека прежде всего стремится восстановиться за счет своих адаптационных возможностей, которые проявляются прежде всего в изменении функций взаимосвязей. Поэтому как сама структура функции, так и ее коэффициенты являются показательными критериями функционального состояния. Более того, модельный подход и эти функции позволяют прогнозировать развитие патологии.
Рассмотрим данный подход для определения состояния системы «сердце-сосуды». Пусть имеются синхронно регистрируемые биосигналы перемещений стенки кровеносного сосуда x и электрической активности сердца (электрокардиосигнала) e. Тогда модель пульсовой активности может быть представлена в виде расширенного уравнения Ван-дер-Поля – Релея [3]:
![]()
Где ![]() - частота основного гармонического колебания стенки сосуда;
- частота основного гармонического колебания стенки сосуда;
![]() – функция, описывающая воздействие сердечной активности на динамику стенки сосуда; e1, e2, w0, r0 – неизвестные параметры, которые находятся на этапе параметрической идентификации модели с помощью метода наименьших квадратов.
– функция, описывающая воздействие сердечной активности на динамику стенки сосуда; e1, e2, w0, r0 – неизвестные параметры, которые находятся на этапе параметрической идентификации модели с помощью метода наименьших квадратов.
Значения ![]() определяются по экспериментально полученным данным.
определяются по экспериментально полученным данным.
Коэффициент а в модели (1) отражает механические свойства сосудов, в частности «жесткость» их стенок. При эластичных (здоровых) сосудах адаптационный механизм человека работает так, что при увеличении нагрузки «жесткость» сосудов изменяется за счет работы обволакивающих их гладких мышц. Исследование модели и проверка ее адекватности приведены в работе [3]. Однако модель хорошо работает только в случае здоровых сосудов.
Высокий уровень холестерина в крови приводит к тому, что его излишки начинают откладываться на стенках сосудов, что может привести к сужению артерий за счет формирования липидных отложений, последующего разрастания соединительной ткани и отложения кальция в стенках сосудов. На ранних стадиях этот процесс обратимый и полоски жира могут исчезнуть, однако в дальнейшем вокруг сгустка холестерина возможно разрастание соединительной ткани, похожей на рубец. Это приводит к изменению механических свойств стенок сосудов. В результате модель (1) теряет свою адекватность, поскольку не учитывает нелинейные процессы, происходящие при сужении артерий и потере эластичности их стенок [4].
В рассматриваемом случае более адекватной становится обобщенная модель в форме уравнения Ван-дер-Поля – Дуффинга, учитывающая подобные эффекты:
![]()
Рассчитанные с помощью моделей (1) или (2) значения параметров a и b функции связи могут рассматриваться как дополнительный диагностический критерий при диагностике функционального состояния человека. При этом модель (2) предназначена для исследования пациентов из групп риска с высоким содержанием холестерина, а модель (1) – для остальных групп пациентов.
Для выявления групп риска будем рассматривать наиболее активную часть взрослого населения. Определим, какая категория из него чаще подвержена заболеваниям, связанным с повышенным содержанием холестерина в крови. Используем имеющиеся статистические данные по заболеваниям желчного пузыря, поскольку повышенное содержание холестерина в первую очередь приводит к подобным заболеваниям.
Рассматриваемая задача выявления групп риска относится к кластеризации (классификации), когда в зависимости от выделенных признаков осуществляется отнесение объектов к одной из групп.
Задача решается в два этапа:
1) определение признаков кластеризации и формирование групп населения по выбранным признакам;
2) анализ частоты заболеваний в каждой выявленной группе населения.
В зависимости от выбранных признаков возможно формирование разного количества групп населения. При выборе признаков кластеризации будем учитывать следующие требования:
- признаки должны быть объективными и характеризовать всю исследуемую часть населения;
- признаки должны быть легко определены без специального медицинского обследования населения;
- количество признаков должно быть невелико.
В результате были выбраны такие признаки кластеризации, как пол, возраст, индекс массы тела. В зависимости от возраста люди были разбиты на 3 группы, в зависимости от индекса массы тела – также на 3 группы. Таким образом, выбранные параметры позволяют разбить население на 18 групп. В качестве критерия отнесения к группе риска использовалась частота заболеваний желчного пузыря.
Была проанализирована случайная выборка людей (151 человек), среди них 16,55% оказались здоровыми и у 83,45% людей были выявлены те или иные заболевания желчного пузыря. Самый молодой пациент 21 год, самый пожилой пациент 79 лет. Все пациенты получали стационарное лечение в терапевтических отделениях Саратовской городской клинической больницы №9 и «Медсанчасти ГУВД по Саратовской области».
Для повышения адекватности результатов были определены диапазоны изменения значений 2-го параметра таким образом, чтобы в каждую возрастную группу попадало примерно одинаковое количество людей. Аналогично были выбраны диапазоны изменения 3-го параметра.
Кодирование признаков осуществлялось следующим образом:
- Пол: 1 – мужской; 2 – женский;
- Возраст: 1 - 20–40 лет, 2 - 41-55, 3 - 56-80;
- Индекс массы тела: 1 - ниже нормы (20– 23,5), 2 – норма (23,6 – 26,5), 3 – выше нормы (26,6 – 32).
Анализ показал, что наибольший процент заболеваний у мужчин в группе 111 (молодых, с недостаточным индексом массы тела) и у женщин – в группе 232 (старшего возраста, с нормальным индексом массы тела).
Далее были рассмотрены группы населения, сформированные по двум признакам: возраст и индекс массы тела (т.е. исключен пол). Результаты представлены в табл. 1.
Таблица 1. Выявление групп риска
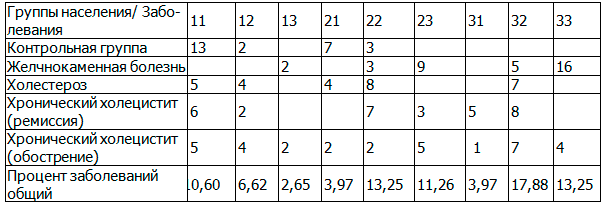
Наибольшее количество заболеваний в группе 32 (старший возраст, нормальный индекс массы тела). Наименьший процент заболеваний в группе 13 (молодые, повышенный индекс массы тела) и 31 (старший возраст, индекс массы тела ниже нормы). Анализ показал, что группами риска заболеваний желчного пузыря являются в молодой возрастной группе люди с недостаточным индексом массы тела. В противоположность, в средней и старшей возрастных группах меньше подвержены указанным заболеваниям люди с недостаточным индексом массы тела.
Выдвинем гипотезу, что с возрастом риск заболеваний снижается при снижении индекса массы тела, т.е. чем меньше возраст, тем выше должен быть индекс массы тела. Разобьем исследуемую выборку людей следующим образом:
- по возрасту на 4 возрастные группы:
1) 21 – 37 лет (37 случаев);
2) 38 – 46 лет (38 случаев);
3) 47 – 59 лет (40 случаев);
4) 60 – 79 лет (36 случаев;
- по индексу массы тела на 3 группы:
1) индекс массы ниже нормы (20 – 23,5) - 49 случаев;
2) индекс массы в норме (23,6 – 26) - 59 случаев;
3) индекс массы выше нормы (26,1 – 32) - 43 случая.
В результате получилось 12 групп населения, результаты представлены в табл. 2 (первый индекс соответствует возрастной группе).
Таблица 2. Частота заболеваний в различных группах
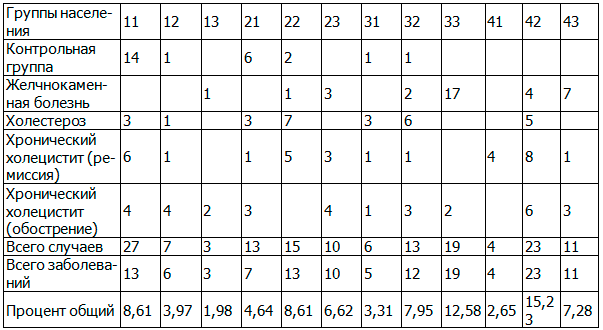
Таким образом, к группам риска действительно следует отнести молодую возрастную группу людей с недостаточным индексом массы тела. В противоположность, в средней и старшей возрастных группах чаще подвержены указанным заболеваниям люди с повышенным индексом массы тела.
Таким образом, выявленные группы риска позволили определить условия применимости моделей (1) и (2), а рассчитанные с их помощью значения коэффициентов функции связи позволят оценить функциональное состояние конкретного человека и определить группы риска по сосудистым заболеваниям.
